Un array es un medio de guardar un conjunto de objetos de la misma clase. Se accede a cada elemento individual del array mediante un número entero denominado índice. 0 es el índice del primer elemento y n-1 es el índice del último elemento, siendo n, la dimensión del array. Los arrays son objetos en Java y como tales vamos a ver los pasos que hemos de seguir para usarlos convenientemente
- Declarar el array
- Crear el array
- Inicializar los elementos del array
- Usar el array
Declarar y crear un array:
Para declarar un array se escribe
tipo_de_dato[ ] nombre_del_array;
Para declarar un array de enteros escribimos
int[ ] numeros;
Para crear un array de 4 número enteros escribimos
numeros=new int[4];
La declaración y la creación del array se puede hacer en una misma línea.
int[ ] numeros =new int[4]
Inicializar y usar los elementos del array:
Para inicializar el array de 4 enteros escribimos
numeros[0]=2;
numeros[1]=-4;
numeros[2]=15;
numeros[3]=-25;
Se pueden inicializar en un bucle for como resultado de alguna operación
for(int i=0; i<4; i++){
numeros[i]=i*i+4;
}
No necesitamos recordar el número de elementos del array, su miembro dato length nos proporciona la dimensión del array. Escribimos de forma equivalente
for(int i=0; i<numeros.length; i++){
numeros[i]=i*i+4;
}
Los arrays se pueden declarar, crear e inicializar en una misma línea, del siguiente modo
int[ ] numeros={2, -4, 15, -25};
String[ ] nombres={"Juan", "José", "Miguel", "Antonio"};
Para imprimir a los elementos de array nombres se escribe
for(int i=0; i<nombres.length; i++){
System.out.println(nombres[i]);
}
Java verifica que el índice no sea mayor o igual que la dimensión del array, lo que facilita mucho el trabajo al programador.
Para crear un array de tres objetos de la clase Rectangulo se escribe
- Declarar
Rectangulo[ ] rectangulos;
- Crear el array
rectangulos=new Rectangulo[3];
- Inicializar los elementos del array
rectangulos[0]=new Rectangulo(10, 20, 30, 40);
rectangulos[1]=new Rectangulo(30, 40);
rectangulos[2]=new Rectangulo(50, 80);
O bien, en una sola línea
Rectangulo[ ] rectangulos={new Rectangulo(10, 20, 30, 40),
new Rectangulo(30, 40), new Rectangulo(50, 80)};
- Usar el array
Para calcular y mostrar el área de los rectángulos escribimos
for(int i=0; i<rectangulos.length; i++){
System.out.println(rectangulos[i].calcularArea());
}
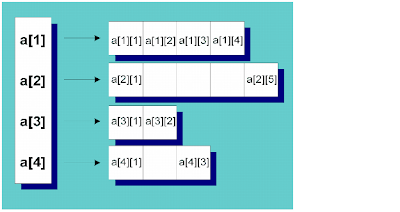
Arrays multidimensionales:
Una matriz bidimensional puede tener varias filas, y en cada fila no tiene por qué haber el mismo número de elementos o columnas. Por ejemplo, podemos declarar e inicializar la siguiente matriz bidimensional
double[ ][ ] matriz={{1,2,3,4},{5,6},{7,8,9,10,11,12},{13}};
La primer fila tiene cuatro elementos {1,2,3,4}
La segunda fila tiene dos elementos {5,6}
La tercera fila tiene seis elementos {7,8,9,10,11,12}
La cuarta fila tiene un elemento {13}
Para mostrar los elementos de este array bidimensional escribimos el siguiente código
for (int i=0; i < matriz.length; i++) {
for (int j=0; j < matriz[i].length; j++) {
System.out.print(matriz[i][j]+"\t");
}
System.out.println("");
}
Como podemos apreciar, matriz.length nos proporciona el número de filas (cuatro), y matriz[i].length, nos proporciona el número de elementos en cada fila.
Mostramos los elementos de una fila separados por un tabulador usando la función print. Una vez completada una fila se pasa a la siguiente mediante println.
Los arrays bidimensionales nos permiten guardar los elementos de una matriz. Queremos crear y mostrar una matriz cuadrada unidad de dimensión 4. Recordaremos que una matriz unidad es aquella cuyos elementos son ceros excepto los de la diagonal principal i==j, que son unos. Mediante un doble bucle for recorremos los elementos de la matriz especificando su fila i y su columna j. En el siguiente programa
- Se crea una matriz cuadrada de dimensión cuatro
- Se inicializa los elementos de la matriz (matriz unidad)
- Se muestra la matriz una fila debajo de la otra separando los elementos de una fila por tabuladores.